Tekst: JOOSEP PATA
Suur hadronite põrguti (Large Hadron Collider, LHC), maailma suurim ja võimsaim osakestekiirendi, asub CERN-is, Šveitsi ja Prantsuse piiri peal. Kuna alates tänavusest aastast on Eesti CERN-i täisliige, on meie võimalused arendada teadust, tehnoloogiat ja ettevõtlust avardunud. CERN on osakestefüüsika uurimise tippkeskus. See on üks väheseid uuenduskeskusi ja -suundi, kus Euroopa on maailmas konkurentsivõimeline.
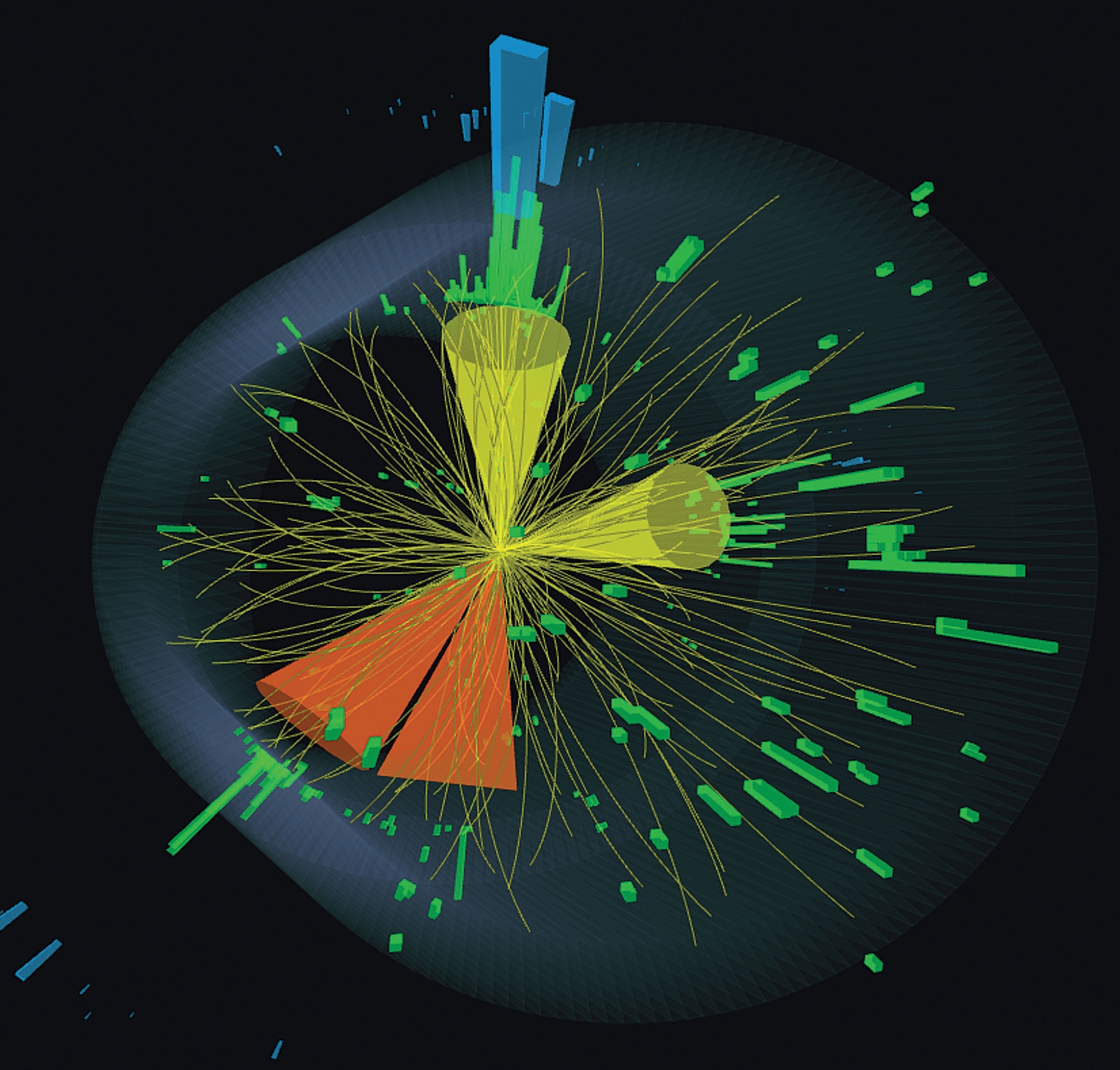
LHC kiirendis põrgatatakse prootoneid miljoneid kordi sekundis. Igast põrkest tekib sadu tuhandeid osakesi, mis kan- navad informatsiooni loodusseaduste kohta väga kõrgetel energiatel või väga varajastel universumi arenguetappidel. Aastal 2012 avastati CERN-is täiesti uut tüüpi osake – ilma spinnita Higgsi boson, mis annab teistele osakestele massi. Need avastused ei sünni iseenesest: iga läbimurre nõuab tohutu hulga andmete töötlemist. LHC detektorid registreerivad sekundis miljoneid põrkeid, seega tekib iga päev petabaitide viisi andmeid, mida tuleb põhjalikult analüüsida. Selline andmeanalüüs muutub aina keerukamaks kahel põhjusel. Esmalt suurendab LHC järkjärguline täiustamine pidevalt andmevoogusid. Lisaks nõuab uute osakeste ja nähtuste otsimine üha täpsemat analüüsi, et eristada haruldasi sündmusi tavapärastest. Praegused arvutussüsteemid jõuavad selle ülesande keerukuse kasvades oma võimete piirile.
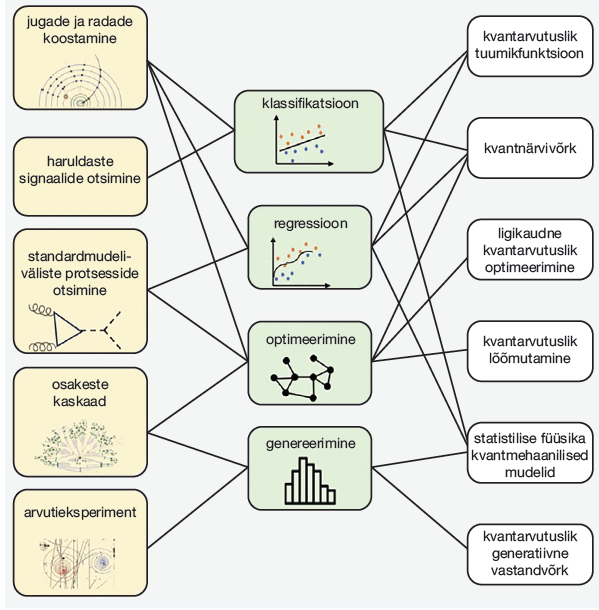
Siin võib tulevikus appi tulla kvantarvuti, mis suudab teatud ülesandeid lahendada tavalisest arvutist ekspo-nentsiaalselt paremini ja kiiremini. Osakestefüüsika andmeid analüüsides on näiteks keeruline rekonstrueerida osakesi, eraldada nõrku signaale taus- tast ning teha praeguste loodusseaduste põhjal andmepõhiseid ennustusi ehk simuleerida tehisandmeid. Praegu kasutatavaid klassikalisi algoritme, mis põhinevad kombinatoorikal, optimeerimisel või masinõppel, saab kvantarvutil tihti lahendada kiiremini.
Sisuliselt rakendatakse teistes valdkon- dades arendatud kvantarvutuse algoritme uudsel viisil, et täita osakestefüüsikaga seotud ülesandeid. Nüüdsed kvantarvutid on võrreldes ülikiirelt arenenud klassikaliste arvutitega küllaltki väikesed: suurimates on mõnikümmend kvantbitti, mõni tuhat kvantmehaanilist loogikaväravat ja arvuti töötab vigadeta kuni millisekundi. Võrdluseks: tavalises sülearvutis on kõik need näitajad peaaegu miljard korda suuremad. Sellegipoolest on mõistlik juba praegu mõelda tuleviku peale, kuna kvantarvutite kiire arengu tõttu on mõningatele ülesannetele juba praegu võimalik leida lahendus tunduvalt kiiremini kui tavaarvutiga. Kvantarvuti ei peagi kõigi nende näitajate poolest tavaarvutit ületama: tema eelis ilmneb teatud tüüpi ülesannete korral, kus ta suudab vastuse leida efektiivsemal viisil. Järgnevalt vaatlemegi, kuidas universumi väikseimate ehituskivide ehk algosakeste uurimine tõukab arendama uusi arvutusmeetodeid. Lähemalt uurime kahte osakestefüüsika ülesannet, mille korral võib tulevikus kvant- arvutitest kasu olla.
Põrkes tekkinud osakeste rekonstrueerimine
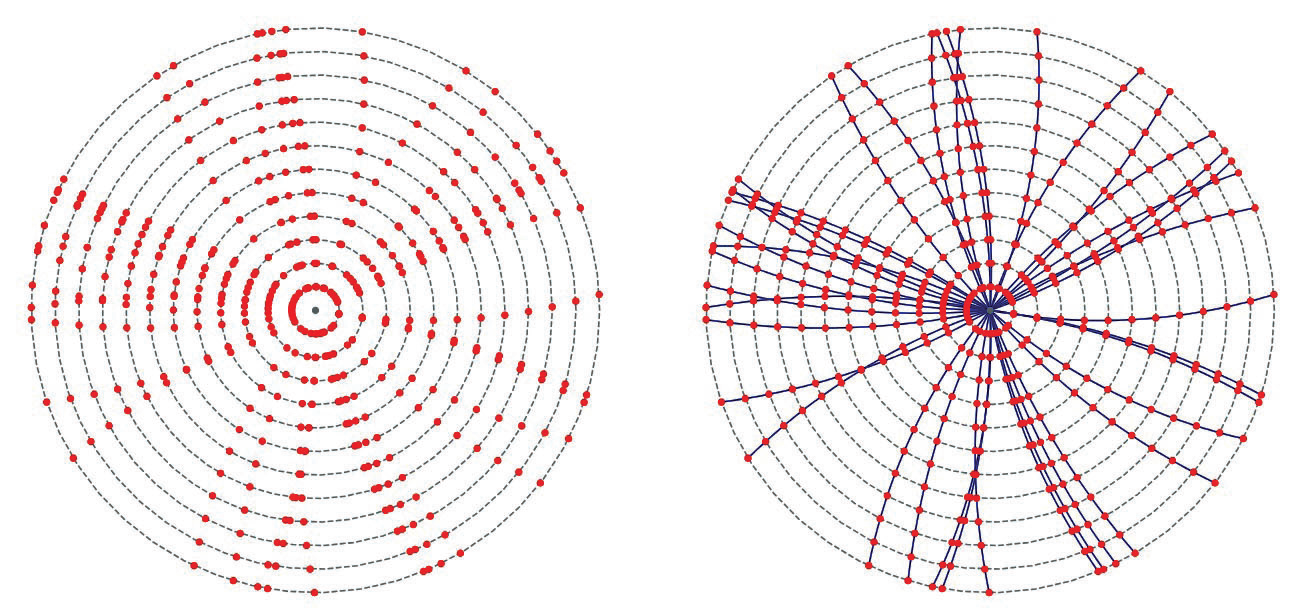
Üks keerukamaid ülesandeid osakestefüüsika andmeanalüüsis on rekonstrueerida laetud osakeste trajektoore ehk radasid. Kui kõrge energiaga prootonid CERN-i kiirendis kokku põrkavad, tekib sadu tuhandeid uusi osakesi, mis lendavad läbi detektori ja jätavad sinna elektrilisi signaale ehk kolmemõõtmeliste pikslitega sarnanevaid detektoritabamusi. Rekonstrueerimisel tuleb need tabamused ühendada radadeks, mis näitavad, millised tabamused kuuluvad samale osakesele. See on raske kombinatoorne ülesanne, kuna ühes põrkes on sadu tuhandeid tabamusi, nendevahelisi võimalikke trajektoore aga eksponentsiaalselt palju.
Klassikaliselt leitakse radu meetodil, mis koosneb mitmest etapist. Kõigepealt leitakse radade algmed, s.o kolm-neli tabamust, mis võiksid kuuluda ühest osakesest lähtunud rajale. Seejärel lisatakse rajale kiht kihi haaval sobivaid tabamusi ja luuakse nende põhjal pikemad rajavariandid. Kolmandas etapis eemaldatakse rajad, millel on liiga palju ühiseid tabamusi, kuna need kirjeldavad tõenäoliselt sama osakest. Lõpuks valitakse välja parima kvaliteediga rajad.
Kvantarvutid võivad siin pakkuda suurt eelist, kuna nad suudavad korraga uurida paljusid tabamuste kombinatsioone. Hiljutiste teadustööde põhjal suudab kvantarvuti teatud radade rekonstrueerimise etappe teha teoks parema skaleeruvusega kui tavaarvuti. Tavalise otsialgoritmiga on kahest tabamusest koosnevate rajaalgmete konst rueerimiseks N tabamuse korral kuluv aeg proportsionaalne tabamuste ruuduga N2. Kui kasutada Groveri indeks- otsingu kvantalgoritmi, mis võimendab kvantmehaaniliselt sobivate paaride tõenäosust, siis on selle ülesande täitmiseks kuluv aeg kõigest √N2 ehk proportsionaalne tabamuste arvuga. Kolmikute leidmisel on need ajad proportsionaal- selt N3 klassikalise algoritmi jaoks ja √N3 kvantalgoritmi jaoks. Siit tuleneb väga märkimisväärne kiiruse vahe, kui tabamuste arv N on suur.
Näiteks kui ühes põrkes on tabamusi 100 000 ja ühe klassikalise võrdluse tarbeks kulub üks nanosekund ja kvant- operatsiooni jaoks üks mikrosekund, siis klassikalise algoritmi korral oleks vaja vastavalt ligikaudu 280 tundi, aga kvantalgoritmil ainult mõnikümmend sekundit. Praktikas saab klassikalise arvutuse muuta kavalate võtete abil efektiivsemaks. Samas on kvantarvuti operatsioonid tavaarvutite omadest üldjuhul aeglasemad. Samuti on vaja kvantarvuti puhul arvestada ajaga, mis kulub kvantolekute ettevalmistamiseks ja väljalugemiseks. Siiski võib väga suurte kombinatoorste ülesannete lahendamine käia tavaarvutile üle jõu, ent kvantarvuti saaks sellega hakkama märksa kergemalt. Tuleb märkida, et praegused kvantarvutid on veel liiga väikesed ja ebatäpsed, et neid CERN-i andmete analüüsimiseks kasutada. Näiteks on vaja kvantalgoritme kohandada, et nad suudaksid töötada ka mürarohke andmestikuga, kus kõiki tabamusi ei pruugi detektoris näha.
Pikemas plaanis võivad kvantarvutid tuua läbimurde osakeste trajektooride rekonstrueerimisel. Kui õnnestub ehitada piisavalt võimsad kvantarvutid, saaks radasid leida palju kiiremini kui tavaarvutitega. See on eriti oluline tuleviku kiirendite jaoks, kus andmete maht ja keerukus suureneb veelgi. Näiteks LHC järgmise edasiarenduse korral kasvab osakeste arv sündmuse kohta praegusega võrreldes kuni viis korda ning radu on veelgi raskem rekonstrueerida. Seega on tähtis juba praegu uurida ja arendada lahendusi, mis suudaksid tuleviku andmehulkadega tõhusalt toime tulla.
Loodusseaduste kontroll tehisandmetega
Kuna kiirendis tekkinud osakesi kirjeldab kvantmehaanika, võib kvantarvutil olla eelis tavaarvuti ees, sest erinevalt tavaarvutist saab osakesi esitada kvant- arvuti jaoks loomulikul kujul, s.o põimitud lainefunktsioonidena. Kiirendi- andmete mõtestamiseks kasutatakse tehisandmeid, mille abil kontrollitakse, kas katsed vastavad loodusseadustele, ja mõõdetakse osakeste omadusi, nagu mass, spinn jne.
Praegu luuakse tehisandmeid klassi- kaliste arvutisimulatsioonidega, mis lähendavad kvantprotsesse (osakeste teket, detektoriga vastastikmõju ja lagunemist) klassikalise tõenäosuse alusel. Ent sedalaadi arvutus on väga mahukas ega saa põhimõtteliselt olla kunagi piisavalt täpne, sest klassikaliselt ei saa kvantprotsesse kunagi kujutada piisava täpsusega. Samas võib kvantarvuti matkida keerulisi protsesse tunduvalt täpsemalt. Ehk sõnastades ümber füüsik Richard Feynmani öeldu: „Pagan võtaks, loodus ei ole klassikaline – kui tahad loodust kirjeldada, siis peab see kirjeldus olema kvantmehaaniline“.
Haruldaste põrgete otsimine ja klassifitseerimine kvantmasinõppega
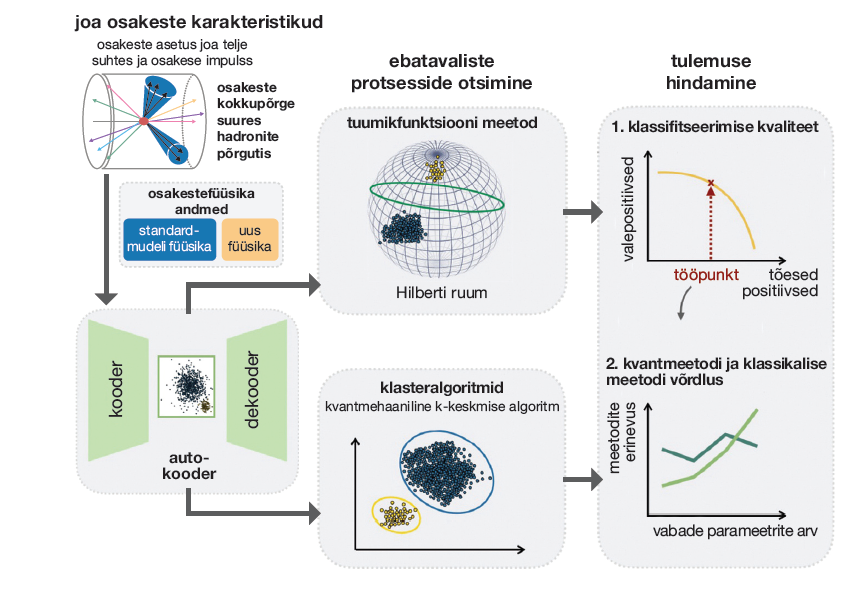
Kuidas saavad neutriinod massi? Mis on tumeaine ja tumeenergia? Pärast Higgsi bosoni avastamist on LHC põhi- eesmärk vastata füüsika veel lahendamata küsimustele. Selleks tuleb põrkest rekonstrueeritud osakeste jaotuste ja mustrite põhjal otsustada, kas põrkes tekkis ka teadaoleva osakestefüüsika ehk nn standarmudeli väliseid osakesi. Tavaliselt käib vastav analüüs nii, et võetakse kogu teadaolev osakestefüüsi- ka ja tekitatakse sellest tohutus koguses tehisandmeid, mida nimetatakse taustaks. Sama tehakse uue füüsika mudelitega ja tekitatakse tehisandmeid, mida nimetakse signaali kandidaatiteks. Tehisandmetes eristatakse signaalikandidaate taustast juhitud masinõppe klassifikatsioonialgoritmide abil. Kui mudel tehisandmetes toimib, siis kasutatakse seda katseandmetes, et näha, kas need uue füüsika mudelid võiksid päriselt kehtida. Niisuguse juhitud masinõppe viisiga saab otsida ainult selliseid uue füüsika nähtusi, millel on mingi teoreetiline alus: me teame, mida me otsime, kuigi me pole seda veel leidnud. Näiteks otsime tumeaine osakesi, sest nende olemasolu on kaudselt tõestatud, ehkki me pole neid kunagi näinud. Aga mismoodi leida täiesti ootamatuid nähtusi, mille võimalikkust pole osatud ette näha? Need võivad olla füüsika seisukohalt palju põnevamad avastused, sest nad viitavad täiesti uutele loodusseadustele.
Anomaaliate otsimise algoritmi põhimõte on, et ei valita välja konkreetseid uue füüsika mudeleid. Selle asemel üritatakse leida iga üles võetud põrke jaoks tõenäosus, kuivõrd see põrkesündmus kattub teadaoleva füüsikaga ehk osakestefüüsika standardmudeliga. Füüsikaprotsessides tekivad raskete osakeste lagunemisel osakeste kimbud ehk joad. Jugades olevate osakeste muster kannab informatsiooni selle kohta, millised osakesed tekkisid. Potentsiaalsed uue füüsika osakesed võivad jätta sellise mustriga jugasid, mida me ei oska tehisandmetes kirjeldada. Küll aga oskame tehisandmete abil hästi kirjel- dada teadaolevat füüsikat ja võime kasutada masinõpet, et ära õppida juba teadaolevatest protsessidest tekkinud jugade mustrid.
Selleks kasutatakse nn autokooderi (ingl autoencoder) algoritmi, mis üritab tehisnärvivõrgupõhise kooderiga jugades olevate osakeste sisendandmeid kokku pakkida, ja siis dekooder-närvivõrguga neid uuesti lahti pakkida. Kui sellist närvivõrkude komplekti treenida teadaolevate protsessidega ehk standardmudeli tehisandmestikul, siis on võimalik teadaolevate protsesside struktuur efektiivselt ära õppida ja suur hulk muutujaid väiksemaks kokku pakkida.
Kooder-närvivõrgu väljund kannab nüüd endas sama informatsiooni nagu algne andmestik, kuid kokkupakitud ja efektiivsemal kujul. Nüüd tulevad appi kvantarvutusel põhinevad masinõppealgoritmid, mis suudavad väheste näidete ja kokkupakitud andmete põhjal hästi eristada teadaolevaid protsesse uutest protsessidest. Kõigepealt on vaja kooder-närvivõrgu väljundid esitada kvantbittide jada ehk kvantregistri kujul. Igat registri kvantbitti pööratakse Blochi sfääril (Blochi sfääriga on või-malik geomeetriliselt kujutada ühe kvantbiti võimalikke seisundeid) kooder-närvivõrgu muutujate paaride alusel ja kvantbitid seatakse omavahel põimitud olekusse. Niimoodi saab väga väikesesse kvantregistrisse, näiteks kuni neli kvantbitti, pakkida väga tõhusalt kokku suure hulga informatsiooni.
Seejärel saab kasutada klassikaliste andmeanalüüsi algoritmide kvantarvutuslikke edasiarendusi, näiteks klasteranalüüsi või toevektormasinaid, et eristada võimalikke uue füüsika protsesse tavafüüsika omadest. Niisuguste algoritmide eelis on ennekõike parem eristamise efektiivsus väga väikeste andmestike või väga kompaktsete sisendmuutujate korral. Kvantarvutus võimendab siin algoritmide efektiivsust väheste andmetega režiimis, kuna kasutab ära sisendmuutujate vahelisi põimitusi. Nõnda saab edukalt kasutada klassikalist masinõpet, et tekitada sisukad algolekud praegustele kvantarvutitele, ja seeläbi parandada haruldaste protsesside otsimisviiside tundlikkust.
Tulevikuväljavaated
Praegu käib vilgas töö, proovides prototüübifaasis kvantarvutitega lahendada osakestefüüsika keerulisi arvutusprob- leeme. Üldpõhimõtte järgi tuleb osakestefüüsika protsessid, näiteks laetud osakeste rekonstrueerimine detektoritabamustest, laadida kvantarvutisse ja sõnastada ülesanne nõnda, et kvantarvuti saaks selle efektiivselt lahendada. Tavaliselt tuleb selleks koostada kombinatoorsed või otsinguülesanded, millele võib klassikalisel arvutil kuluda ülemäära palju aega. Selliste ülesannete jaoks on võimalik kasutada juba välja töötatud kvantalgoritme, näiteks kvantarvutusel põhinevat Groveri otsimisalgoritmi, mis lahendavad keerukaid kombinatoorseid ülesandeid tõhusamalt.
Lähituleviku kvantarvutid on tõenäoliselt liiga väikesed ja liiga suurte vigadega, et neist võiks osakestefüüsika andmetöötluses praktilist kasu olla. Küll aga on võimalik selleks juba praegu välja töötada uudseid võtteid ja oskusteavet. Kui kvantarvutid jõuavad laialdaselt kasutusele, siis on võimalik praeguste arenduste põhjal loodud ra- kendustega kiiresti edasi liikuda. Kuna masinõpet kasutatakse nii osakestefüüsikas kui ka ühiskonnas üldiselt väga palju, on kvantarvutusel põhinev masinõpe eriti paljulubav arengusuund. Sisu- liselt on võimalik luua hübriidmeeto- deid, millega saab klassikalisi masinõppel põhinevaid algoritme kasutada kvantarvuti abil kiiremini ja efektiivsemalt. Haruldaste osakestefüüsika protsesside otsimise kõrval saab niisuguseid algoritme rakendada ka mujal, kus on vaja otsida suurtest andmestikest nõrka signaali.
Joosep Pata (1990) on füüsik, keemilise ja bioloogilise füüsika instituudi vanemteadur. Uurib masinõppe ja kõrgjõudlusarvutuse meetodite rakendamist osakestefüüsikas