Tekst: PEETER SAARI
Võib väita, et mittelineaarne optika on kvantmehaanika juubeli tähistamisel mõneti kontvõõras. Kvantmehaanika põhivõrrandid on lineaarsed. Pealegi, erinevalt näiteks kvantoptikast, mis sündis koos kvantmehaanikaga, võinuks mittelineaarne optika kui teadusala teoreetiliselt tekkida juba 19. sajandil klassikalise füüsikalise optika raames. Kuivõrd on selles ketserlikus väites tõtt, selgub kirjutisest.
Alustame terminite tähendusest. „Mittelineaarne“ on üha moekam sõna, mida ohtralt kasutatakse paljudes valdkondades. Näiteks räägitakse „mittelineaarsest mõtlemisest“, mis olevat omane neuroloogiliste eripäradega inimestele. Kes küll saaks täielikult aru, mida see tähendab? Kas see võib aidata kvantmehaanikat mõista?
Signaalide ja süsteemide teoorias, elektroonikas ja füüsikas üldiselt tähendab lineaarsus lihtsalt öeldes seda, et kui sisendiks on sinusoidaalne ehk harmooniline võnkumine, siis väljundis ei ole muud kui seesama võnkumine, ehkki amplituud ja võnkefaas võib olla muutunud. Uusi sagedusi lineaarses süsteemis ei teki. Näiteks on takistitest, kondensaatoritest ja induktiivpoolidest kokku pandud suvaline elektroonikasüsteem just sellises tähenduses lineaarne. Nagu ka (kvaliteetne) helivõimendi, hoolimata tema tämbri muutmise nuppudest, võimalusest lisada kajaefekt jms. Põhimõtteliselt samuti on klassikalises optikas, kus väljundvalguse annab pealelangeva valguse tekitatud lineaarne polarisatsioon, mis pole muud kui võnkumise tekitamine ainetüki mikroosakestes. Muidugi on asi keerulisem kui elektroonikaskeemis, kas või see- tõttu, et signaaliks on kolmemõõtmelises ruumis leviv laine ja takistused; mahtuvused ning induktiivsused on ruumis laiali jaotatud.
Elektroonikast või elektrotehnikast leiame hästi tuntud alaldava dioodi kui lihtsaima, kuid tugevalt mittelineaarse skeemielemendi. Vool dioodis pole proportsionaalne sisendpingega, kui see märki muudab. Seetõttu sisaldab alaldatud ehk raadiosignaali puhul demoduleeritud väljund peale sisendi sageduse selle kordseid võnkumisi ehk kõrgemaid harmoonilisi ehk ülemtoone ja muidugi ka nullise sagedusega alaliskomponenti.
Põhimõtteliselt samuti muutub lineaarne optika mittelineaarseks, kui vaid leida materjal, mille polarisatsiooniline koste langevale valgusele on mitte- lineaarne. Asjaomane teooria võinuks olla kirja pandud ammu enne kvant- mehaanika sündi ja viimast vajamata. Tegelikkuses arendas mittelineaarse optika süstemaatilise teooria 1960. aas- tail välja hollandi päritolu Ameerika füüsik Nicolaas Bloembergen, kes sai selle eest Nobeli auhinna 1981. aastal. Varem oli puudunud piisavalt võimas ja n-ö puhas optiline laine, mille toimel tuleks esile ainete polarisatsiooni mitte- lineaarsus. Seepärast oli mittelineaarse optika kümneid efekte, sh optiline alaldamine, võimalik avastada pärast laseri leiutamist. Praegusajal on igaüks, kes on käes hoidnud rohelise kiirega laserosutit, kasutanud tuntuimat mitte- lineaarse optika nähtust – teise harmoonilise genereerimist –, sest pointeris muudetakse väikese neodüümlaseri infrapunakiirsageduse kahekordistamise teel kristallitükis roheliseks.
Aga enne kui akronüüm LASER saipärast 1960. aastaid valdavaks, oli selle riistapuu nimetus „optiline kvantgeneraator“. Kas seega pole kvantmehaanika geenid mittelineaarses optikas esinda- tud tugevamini, kui loo alguses sai väidetud? Nii ja naa… Ühelt poolt on monokromaatne laserivalgus nii lähedane kui võimalik – peaaegu eristamatult – klassikalise elektrodünaamika ettekujutustele võnkuvast elektromag- netväljast ning on praktiliselt sama puhas sinusoid nagu raadiolaine. Ent teiselt poolt pole laseri toimimise aluseks olev sundkiirgus võimalik klassikalises mudelis, kus laengud võnguvad mikro- osakestest aines (muide, isegi siis mitte, kui need võnkumised kvantmehaanika kohaselt kvantiseerida). Sundkiirgus saab tekkida spetsiifiliselt paiknevate kvant-energiatasemete eri tõenäosustega asustamisel aines, aga diskreetsed energiatasemed on teadagi kvant- mehaanika…
Senise kokkuvõtteks. Tavaliste valgustugevuste korral on aines tekkiv polarisatsioon lineaarne, uusi sagedusi väljundisse tekkida ei saa (jätame kõrvale luminestsentsi ja spontaanse hajumise, mida käsitletakse teistsuguses paradigmas). Mittelineaarses optikas aga saab, mis muu hulgas tähendab või- malust suruda valgusimpulss palju lühemaks, kui seda lubaks sisendimpulsi spektraalne koostis. Kvantmehaanika saab kokku mittelineaarse optikaga – ja ka lineaarsega –, kui on vaja välja arvutada aine polarisatsiooni eri järku liikmed. Veelgi enam tugevneb nende kahe teadusvaldkonna seos, kui me käsitleme suurema täpsuse ja süsteemsuse huvides ka valgust kvantväljana. Seega tuleb artikli alguse ketserlikku väidet pehmendada.
Nüüd aga käsitleme mittelineaarse optika nähtust, kus kvantmehaanikat pole vaja mitte täpsuse pärast, vaid kus ta mängib nähtuse mõistmises põhimõttelist rolli. See on nn kõrgete harmooniliste ja atosekundiliste impulsside genereerimine. Asjaomaste eksperimentaalsete saavutuste eest said prantslased Pierre Agostini ja Anne L’Huillier ning ungari-saksa füüsik Ferenc Krausz eelmisel aastal Nobeli auhinna.
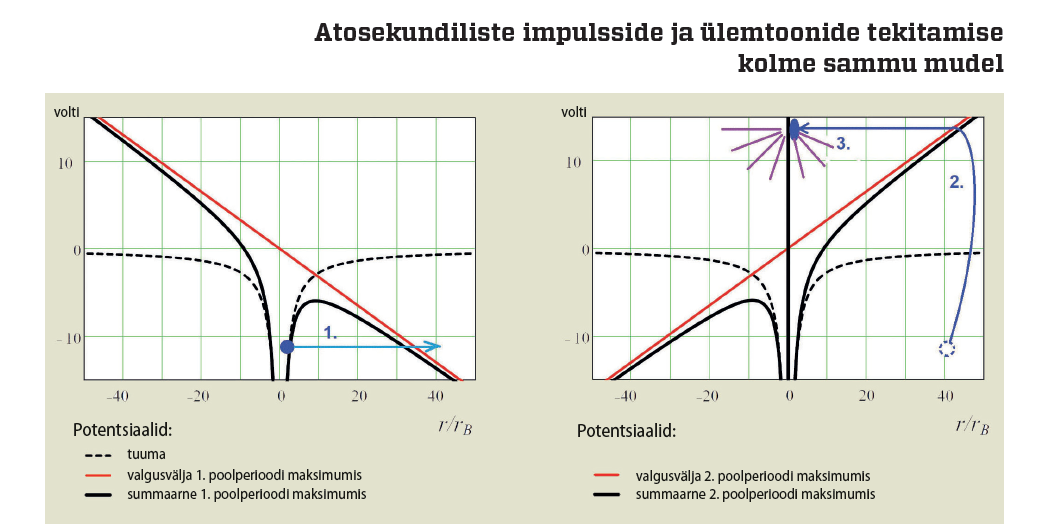
Juuresoleva infokasti potentsiaaligraafikute kohta tuleb märkida, et neil on üks puudus ja üks hea omadus. Puudus on tegelikkuses kolmemõõtmelises ruumis oleva potentsiaali kujutamine ainult ühest koordinaadist sõltuvana. Ent kui kolme ruumikoordinaati isegi kujutada kabinet- vm projektsiooni abil lehekülje tasandil, siis kuhu suunata neljas, volte näitav graafikutelg? Hea omadus on aga analoogia asukoha- punkti kõrguse ja seeläbi raskusjõu potentsiaalse energiaga mägede ja orgudega maastikul. Seetõttu on kohe ilmselge, et joonisel (a) kujutatud elektron ei saa klassikalise mehaanika järgi lahkuda tuuma juurest üle potentsiaali- mäe, sest tal ei jätku selleks energiat. Kvantmehaanika aga lubab tal teatava tõenäosusega potentsiaalibarjäärist läbi tungida. See nn tunneliefekt, mille avastas juba 1927. aastal Saksa füüsik Hermann Hund, kuulub kvantmehaanika raudvarasse ja seletub mikroosakeste laineomadustega. Ja loomulikult on kvantmehaanika see, mis joonisel (a) ei lase elektronil kukkuda tuuma põhjatusse potentsiaaliauku, vaid hoiab ta energiatasemest olenevalt mingil keskmisel kaugusel tuumast. Edasise mõistmiseks joonisel (b) piisab aga klassikalisest elektrodünaamikast: muutunud suunaga elektriväli kiirendab elektroni tuuma suunas ja sellel äkki pidurdudes tekib nn pärsskiirgus (ingl bremsstrahlung; on tähelepanuväärne, et ingliskeelses füüsikas kasutatakse selle ja veel mõne termini saksakeelset kuju, justkui tunnustades Saksa füüsika liidrirolli saja aasta taguses maailmas). Pärsskiirgus on muide põhiline röntgenikiirguse allikas meditsiiniaparatuuris, kus elektrone kiirendatakse makroskoopilise kõrgepingelise elektriväljaga.
Kuna laserikiire elektrivälja lainepikkus on palju suurem kui aatomite vahekaugus gaasis, rääkimata vedelikest ja tahkistest, mida juba kasutataksegi asjaomasel eesmärgil, muudab elektriväli märki korraga paljude aatomite asukohas ning tulemusena panustavad nad kõik pärsskiirguse impulssi. Infra- punalaseri elektrivälja võnkeperiood on mõne femtosekundi (10-15 s) suurusjärgus, niisiis kordub kogu protsess sama perioodiga ning tekib jada atosekundilisi (10-18 s) impulsse. Laserivälja sagedusega korduvus avaldub aga tekitatud kiirguse suure ulatusega spektris laseri- sageduse kõrgemate harmooniliste ehk ülemtoonide jadana, mis tuleneb juba üldistest signaalide sagedus- ja aegesituse (Fourier’) seostest. Seega, kolme sammu mudel, mida nimetatakse ka poolklassikaliseks, sest sammud 2 ja 3 on mõistetavad kvantmehaanikatagi, selgitab vaatlusaluse nähtuse vähemasti heas lähenduses ära.
Kui uurida joonist põhjalikumalt, võib järeldada: piisavalt tugeva laseri- valguse korral moondub tuuma potentsiaal sedavõrd, et elektroni tuumast eemaldamiseks pole tunneliefekti vajagi: laseri elektriväli lihtsalt rebib ta toore jõuga tuumast eemale ja järgneval poolperioodil paiskab tagasi vastu tuuma. Kas sel juhul pole kvantmehaanikat vajagi? Jah, kuid esiteks, Nobeli auhinna vääriliste uurimuste tegemise ajal vähemasti nii võimsaid lasereid polnud. Teiseks, kas kvantmehaanikata ei kao ka protsessi ilu? Tegelikult n-ö korralikus kvantitatiivses käsitluses kirjeldatakse kogu protsessi läbinisti kvantmehaanika aparaadi abil, ehkki laserivalguse kirjeldus on jäetud klassikaliseks. Kuid ainult seniks… Nimelt on tippajakirja Nature Physics oktoobrinumbris ilmunud uurimus kõrgete har- mooniliste ehk ülemtoonide genereerimisest Mg:LiNbO3 kristallitükis, millele oli suunatud eriline valgusväli, nn ere muljutud vaakum (brigth squeezed vacuum). Me ei püüagi siinkohal avada selle sügavalt kvantoptikasse kuuluva termini sisu, kuid võtame teadmiseks, et sellise eksootilise valguse abil muutub kõrgete harmooniliste tekitamine oluliselt tõhusamaks.
Milleks siis mõnekümne atosekundi kestusega impulsid head on? Olgu märgitud, et atosekund on nii lühike ajavahemik, et ühte sekundisse mahub neid umbes sama palju, kui on möödunud sekundeid universumi algusest. Atosekundid on atomaarne ajaskaala. Seega, niivõrd lühikesed impulsid annavad võimaluse vahetult jälgida ja uurida liikumisi aatomite sees ja molekulides. Peale mikroosakeste füüsika sügavama mõistmise tõotab kõrgete harmooniliste genereerimine ja manipuleerimine atosekundiliste impulssidega olla kasulik uute materjalide ja ravimite loomisel, kui nimetada vaid mõnda kiiresti areneva atosekundteaduse olulist praktilist rakendust.
Kvantmehaanika on matemaatilises mõttes küll lineaarne, kuid võib-olla tuleb temast mõelda mittelineaarselt? Teoreetilise füüsika korüfee Richard Feynman on kord pillanud lause: „Ma arvan, et võin julgelt öelda, et keegi ei mõista kvantmehaanikat.“ Kvantmehaanika alusepanijaid Niels Bohr on maininud: ,,Kui kvantmehaanika teid segadusse ei aja, pole te sellest tegelikult aru saanud.“
Jääb vaid tõdeda, et mittelineaarne optika ja kvantmehaanika pole üksteisele võõrad, vaid seda tihedamini põimuvad füüsikaharud, mida eksootilise- maid valgusvälju rakendatakse. Üldse, parafraseerides tuntud Murphy seadust „Kui see ei toimi, siis see on füüsika“, väidame lõpetuseks: „Kui se’s ei ole kvantmehaanikat, siis see pole füüsika.“
Peeter Saari (1945) on füüsik, Tartu ülikooli emeriitprofessor ning Eesti teaduste akadeemia ja Euroopa teaduste akadeemia liige. Üks tema uurimisvaldkondi on olnud füüsikaline optika.